1. What is Non-Linear SVMs?
- In practice, we can be faced with non-linear class boundaries.
- We need to consider enlarging the feature space using functions of the predictors such as quadratic and cubic terms, in order to address this non-linearity.
- In the case of the support vector classifier, we can also enlarge the feature space using quadratic, cubic, and even higher-order polynomial functions of the predictors.
1.1 Feature Expension
- Enlarge the space of features by including transformations : \(X_1^2, X_1^3, ...\).
- For example, \(\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_1^2 + \beta_4 X_2^2 + \beta_5 X_1 X_2 = 0\), This leads to non-linear decision boundaries in the original space.
- The support vector classifier in the enlarged space solves the problem in the lower-dimensional space.
1.2 Computational Issues for High-dimensional Polynomials
- However, high-dimensional polynomials get wild rather fast.
- There are many possible ways to enlarge the feature space, but computations would become unmanageable for a huge number of features.
- There is a more elegant and controlled way to introduce nonlinearities in support vector classifiers, using kernels.
1.3 Kernels and Support Vector Machines
- The linear support vector classifier can be represented as : \(f(x) = \beta_0 + \sum_{i \in S} \hat{\alpha}_i K(x, x_i)\).
- \(S\) is the support set of indicies \(i\) such that \(\alpha_i > 0\).
- Parameters :
- \(\alpha_1, ..., \alpha_n\)
- \(\beta_0\)
- \((n, 2)\) inner products - A generalization of the inner product of the form \(K(x_i, x_{i'})\) is called a kernel.
- kernel is a function that quantifies the similarity of two observations.
1.4 Examples of Kernels
- Standard linear kernel : \(K(x_i, x_{i'}) = \sum_{j=1}^p x_{ij}x_{i'j}\)
- Polynomial kenrel of degree \(d > 1\) : \(K(x_i, x_{i'}) = (1 + \sum_{j=1}^p x_{ij}x_{i'j})^d\)
- We need to tune parameter d
- Radial kernel : \(K(x_i, x_{i'}) = exp(-\gamma \sum_{j=1}^p(x_{ij} - x_{i'j})^2)\)
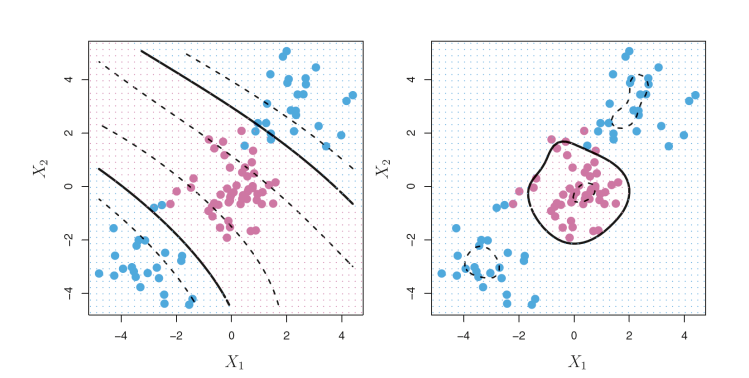
2. Non-Linear Support Vector Classifier
2.1 [Ex] Non-linear SVMs with radial kernel
# Simulate non-linear data set
library(e1071)
set.seed(1)
x <- matrix(rnorm(200*2), ncol=2)
x[1:100, ] <- x[1:100, ] + 2
x[101:150, ] <- x[101:150, ] - 2
y <- c(rep(-1, 150), rep(1, 50))
dat <- data.frame(x, y=as.factor(y))
plot(x, col=y+3, pch=19)
# Training svm model with radial kernel with r=0.5, C=0.1
fit <- svm(y~.,data=dat, kernel="radial", gamma=0.5, cost=0.1)
plot(fit, dat)
summary(fit)
# Training svm model with radial kernel with r=0.5, C=5
fit <- svm(y~.,data=dat, kernel="radial", gamma=0.5, cost=5)
plot(fit, dat)
summary(fit)
# Visualize of test grid for radial kernel with r=0.5, C=1
fit <- svm(y~.,data=dat, kernel="radial", gamma=0.5, cost=1)
px1 <- seq(round(min(x[,1]),1), round(max(x[,1]),1), 0.1)
px2 <- seq(round(min(x[,2]),1), round(max(x[,2]),1), 0.1)
xgrid <- expand.grid(X1=px1, X2=px2)
ygrid <- as.numeric(predict(fit, xgrid))
ygrid[ygrid==1] <- -1
ygrid[ygrid==2] <- 1
plot(xgrid, col=ygrid+3, pch = 20, cex = .2)
points(x, col = y+3, pch = 19)
pred <- predict(fit, xgrid, decision.values=TRUE)
func <- attributes(pred)$decision
contour(px1, px2, matrix(func, length(px1), length(px2)),
level=0, col="purple", lwd=2, lty=2, add=TRUE)
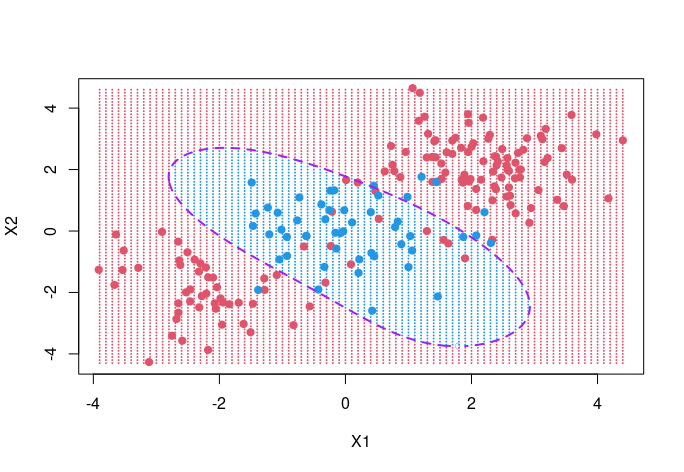
2.2 [Ex] Optimizing non-linear SVMs(radial kernel) using validation set
# Calculate missclassification error of validation set
# Separate training and test sets
set.seed(1234)
tran <- sample(200, 100)
test <- setdiff(1:200, tran)
# Training with hyperparameter tuning of gamma, C
gamma <- c(0.5, 1, 5, 10)
cost <- c(0.01, 1, 10, 100)
R <- NULL
for (i in 1:length(gamma)) {
for (j in 1:length(cost)) {
svmfit <- svm(y~., data=dat[tran, ], kernel="radial",
gamma=gamma[i] , cost=cost[j])
pred <- predict(svmfit, dat[test, ])
R0 <- c(gamma[i], cost[j], mean(pred!=dat[test, "y"]))
R <- rbind(R, R0)
}
}
# Check results
colnames(R) <- c("gamma", "cost", "error")
rownames(R) <- seq(dim(R)[1])
R
# Training with hyperparameter tuning of gamma, C using tune function
set.seed(1)
tune.out <- tune(svm, y~., data=dat[tran, ], kernel="radial",
ranges=list(gamma=gamma, cost=cost))
summary(tune.out)
tune.out$best.parameters
# Calculate missclassification error rate of test sets
pred <- predict(tune.out$best.model, dat[test,])
table(pred=pred, true=dat[test, "y"])
mean(pred!=dat[test, "y"])
- best parameters : gamma(0.5), cost(1)
- Missclassification error rate : 0.09
2.3 [Ex] Optimizing non-linear SVMs(polynomials) using validation set
degree <- c(1, 2, 3, 4)
R <- NULL
for (i in 1:length(degree)) {
for (j in 1:length(cost)) {
svmfit <- svm(y~., data=dat[tran, ], kernel="polynomial",
degree=degree[i] , cost=cost[j])
pred <- predict(svmfit, dat[test, ])
R0 <- c(degree[i], cost[j], mean(pred!=dat[test, "y"]))
R <- rbind(R, R0)
}
}
colnames(R) <- c("degree", "cost", "error")
rownames(R) <- seq(dim(R)[1])
R
tune.out <- tune(svm, y~., data=dat[tran, ], kernel="polynomial",
ranges=list(degree=degree, cost=cost))
summary(tune.out)
tune.out$best.parameters
pred <- predict(tune.out$best.model, dat[test,])
table(pred=pred, true=dat[test, "y"])
mean(pred!=dat[test, "y"])
- best parameters : degree(2), cost(10)
- Missclassification error rate : 0.16
2.4 [Ex] Optimizing non-linear SVMs(sigmoid) using validation set
R <- NULL
for (i in 1:length(gamma)) {
for (j in 1:length(cost)) {
svmfit <- svm(y~., data=dat[tran, ], kernel="sigmoid",
gamma=gamma[i] , cost=cost[j])
pred <- predict(svmfit, dat[test, ])
R0 <- c(gamma[i], cost[j], mean(pred!=dat[test, "y"]))
R <- rbind(R, R0)
}
}
colnames(R) <- c("gamma", "cost", "error")
rownames(R) <- seq(dim(R)[1])
R
tune.out <- tune(svm, y~., data=dat[tran, ], kernel="sigmoid",
ranges=list(gamma=gamma, cost=cost))
summary(tune.out)
tune.out$best.parameters
pred <- predict(tune.out$best.model, dat[test,])
table(pred=pred, true=dat[test, "y"])
mean(pred!=dat[test, "y"])
- best parameters : gamma(0.5), cost(0.01)
- Missclassification error rate : 0.29
2.5 [Ex] Simulation study using different kernels of 20 replications
# Set reps and RES matrix
set.seed(123)
N <- 20
RES <- matrix(0, N, 3)
colnames(RES) <- c("radial", "poly", "sigmoid")
# Training model with calculate missclassification error rate
for (i in 1:N) {
tran <- sample(200, 100)
test <- setdiff(1:200, tran)
tune1 <- tune(svm, y~., data=dat[tran, ], kernel="radial",
ranges=list(gamma=gamma, cost=cost))
pred1 <- predict(tune1$best.model, dat[test,])
RES[i, 1] <- mean(pred1!=dat[test, "y"])
tune2 <- tune(svm, y~., data=dat[tran, ], kernel="polynomial",
ranges=list(degree=degree, cost=cost))
pred2 <- predict(tune2$best.model, dat[test,])
RES[i, 2] <- mean(pred2!=dat[test, "y"])
tune3 <- tune(svm, y~., data=dat[tran, ], kernel="sigmoid",
ranges=list(gamma=gamma, cost=cost))
pred3 <- predict(tune3$best.model, dat[test,])
RES[i, 3] <- mean(pred3!=dat[test, "y"])
}
# Check statistical reports
apply(RES, 2, summary)
| Statistics | radial | poly | sigmoid |
| Min | 0.07 | 0.14 | 0.17 |
| 1st | 0.1 | 0.1675 | 0.2375 |
| Median | 0.12 | 0.1950 | 0.26 |
| Mean | 0.123 | 0.209 | 0.2705 |
| 3rd | 0.1425 | 0.235 | 0.29 |
| Max | 0.18 | 0.31 | 0.43 |
3. Non-linear Support Vector Classifier on Heart dataset
Step 1 : Prepare Heart Dataset
# Prepare Heart dataset
url.ht <- "https://www.statlearning.com/s/Heart.csv"
Heart <- read.csv(url.ht, h=T)
summary(Heart)
Heart <- Heart[, colnames(Heart)!="X"]
Heart[,"Sex"] <- factor(Heart[,"Sex"], 0:1, c("female", "male"))
Heart[,"Fbs"] <- factor(Heart[,"Fbs"], 0:1, c("false", "true"))
Heart[,"ExAng"] <- factor(Heart[,"ExAng"], 0:1, c("no", "yes"))
Heart[,"ChestPain"] <- as.factor(Heart[,"ChestPain"])
Heart[,"Thal"] <- as.factor(Heart[,"Thal"])
Heart[,"AHD"] <- as.factor(Heart[,"AHD"])
summary(Heart)
dim(Heart)
sum(is.na(Heart))
Heart <- na.omit(Heart)
dim(Heart)
summary(Heart)
Step 2 : Separate training and test sets
# Separate training and test sets
set.seed(123)
train <- sample(1:nrow(Heart), nrow(Heart)/2)
test <- setdiff(1:nrow(Heart), train)
Step 3 : Training using SVMs
# SVM with a linear kernel
tune.out <- tune(svm, AHD~., data=Heart[train, ],
kernel="linear", ranges=list(
cost=c(0.001, 0.01, 0.1, 1, 5, 10, 100)))
heart.pred <- predict(tune.out$best.model, Heart[test,])
table(heart.pred, Heart$AHD[test])
mean(heart.pred!=Heart$AHD[test])
# SVM with a radial kernel
tune.out <- tune(svm, AHD~., data=Heart[train, ],
kernel="radial", ranges=list(
cost=c(0.1,1,10,100), gamma=c(0.5,1,2,3)))
heart.pred <- predict(tune.out$best.model, Heart[test,])
table(heart.pred, Heart$AHD[test])
mean(heart.pred!=Heart$AHD[test])
# SVM with a polynomial kernel
tune.out <- tune(svm, AHD~.,data=Heart[train, ],
kernel="polynomial", ranges=list(
cost=c(0.1,1,10,100), degree=c(1,2,3)))
heart.pred <- predict(tune.out$best.model, Heart[test,])
table(heart.pred, Heart$AHD[test])
mean(heart.pred!=Heart$AHD[test])
# SVM with a sigmoid kernel
tune.out <- tune(svm, AHD~.,data=Heart[train, ],
kernel="sigmoid", ranges=list(
cost=c(0.1,1,10,100), gamma=c(0.5,1,2,3)))
heart.pred <- predict(tune.out$best.model, Heart[test,])
table(heart.pred, Heart$AHD[test])
mean(heart.pred!=Heart$AHD[test])
| kernels | Missclassification error rate |
| linear | 0.2214765 |
| radial | 0.2080537 |
| polynomials | 0.2080537 |
| sigmoid | 0.2147651 |
Step 4 : Simulation study using different kernels of 20 replications
set.seed(123)
N <- 20
Err <- matrix(0, N, 5)
for (i in 1:N) {
train <- sample(1:nrow(Heart), floor(nrow(Heart)*2/3))
test <- setdiff(1:nrow(Heart), train)
g1 <- randomForest(x=Heart[train,-14], y=Heart[train,14],
xtest=Heart[test,-14], ytest=Heart[test,14], mtry=4)
Err[i,1] <- g1$test$err.rate[500,1]
g2 <- tune(svm, AHD~., data=Heart[train, ], kernel="linear",
ranges=list(cost=c(0.001, 0.01, 0.1, 1, 5, 10, 100)))
p2 <- predict(g2$best.model, Heart[test,])
Err[i,2] <- mean(p2!=Heart$AHD[test])
g3 <- tune(svm, AHD~., data=Heart[train, ], kernel="radial",
ranges=list(cost=c(0.1,1,10,100), gamma=c(0.5,1,2,3)))
p3 <- predict(g3$best.model, Heart[test,])
Err[i,3] <- mean(p3!=Heart$AHD[test])
g4 <- tune(svm, AHD~.,data=Heart[train, ],kernel="polynomial",
ranges=list(cost=c(0.1,1,10,100), degree=c(1,2,3)))
p4 <- predict(g4$best.model, Heart[test,])
Err[i,4] <- mean(p4!=Heart$AHD[test])
g5 <- tune(svm, AHD~.,data=Heart[train, ],kernel="sigmoid",
ranges=list(cost=c(0.1,1,10,100), gamma=c(0.5,1,2,3)))
p5 <- predict(g5$best.model, Heart[test,])
Err[i,5] <- mean(p5!=Heart$AHD[test])
}
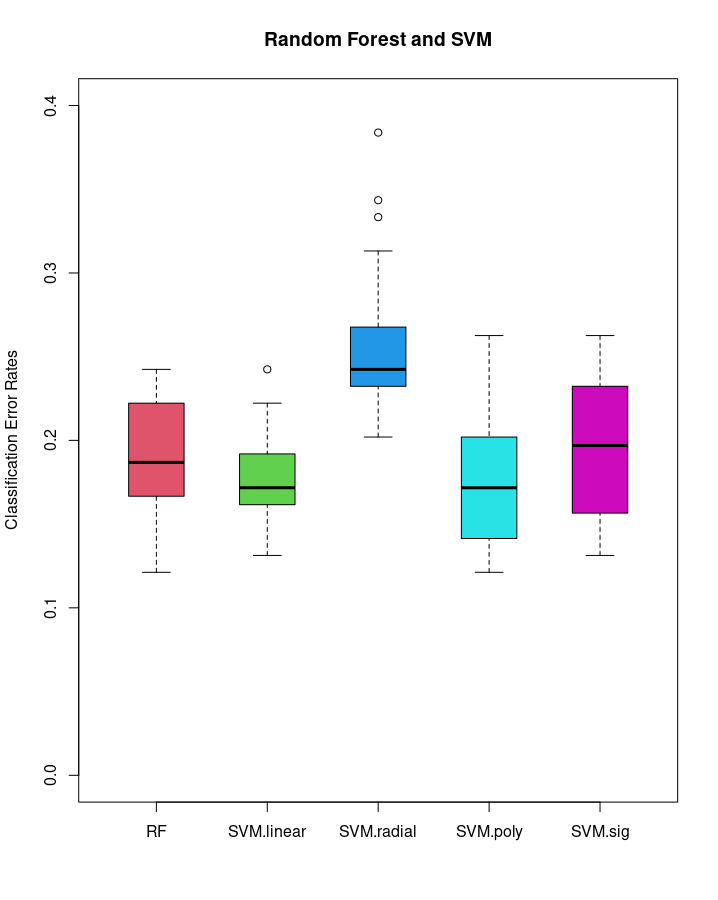
# Visualize results
labels <- c("RF","SVM.linear","SVM.radial","SVM.poly","SVM.sig")
boxplot(Err, boxwex=0.5, main="Random Forest and SVM", col=2:6,
names=labels, ylab="Classification Error Rates",
ylim=c(0,0.4))
colnames(Err) <- labels
apply(Err, 2, summary)
'Data Science > R' 카테고리의 다른 글
| [R] Support Vector Machine (0) | 2022.12.06 |
|---|---|
| [R] Tree-Based Methods : Bayesian Additive Tree (0) | 2022.11.27 |
| [R] Tree-Based Methods : Boosting (0) | 2022.11.27 |
| [R] Tree-Based Methods : Random Forest (0) | 2022.11.27 |
| [R] Tree-Based Methods : Bagging (0) | 2022.11.27 |



