1. Binary Classification
Classification into one of two classes is a common machine learning problem. We might want to predict whether or not a customer is likely to make a purchase, whether or not a credit card transaction was fadulent, whether deep space signals show evidence of a new planet, or a medical test evidence of a disease. These are all binary classification problems.
In our raw data, the classes might be represented by string like "Yes" or "No", or "Dog" and "Cat". Before using this data we'll assign a class label : one class will be 0 and the other will be 1. Assigning numeric labels puts the data in a form a neural network can use.
2. Accuracy and Cross-Entropy
Accuracy is one of the many metrics in use for measuring success on a classification problem. Accuracy is the ratio of correct predictions to total predictions : \(accuracy = \frac{number correct}{total}\). A model that always predicted correectly would have an accuracy score of 1.0. All else being equal, accuracy is a reasonable metric to use whenever the classes in the dataset occur with about the same frequency.
The problem with accuracy (and most other classification metrics) is that it can't be used as a loss fucntion. SGD needs a loss function that changes smoothly, but accuracy, being a ratio of counts, changes in "jumps". So, we have to choose a substitute to act as the loss function. This is the cross-entropy function.
For classification, what we want is a distance between probabilities, and this is what cross-entropy provides. Cross-entropy is a sort of measure for the distance from one probability distribution to another.
The idea is that we want our network to predict the correct class with probability 1.0. The further away the predicted probability is from 1.0, the greater will be the cross-entropy loss. The technical reasons we use cross-entropy are a bit subtle, but the main thing to take away from this sections is just this : use cross-entropy for a classification loss; other metrics we might care about will tend to improve along with.
3. Making probabilities with the Sigmoid Function
The cross-entropy and accuracy function both require probabilities as inputs, meaning, number from 0 to 1. To convert the real-valued outputs produced by a dense layer into probabilities, we attach a new kind of activation function, the sigmoid function.
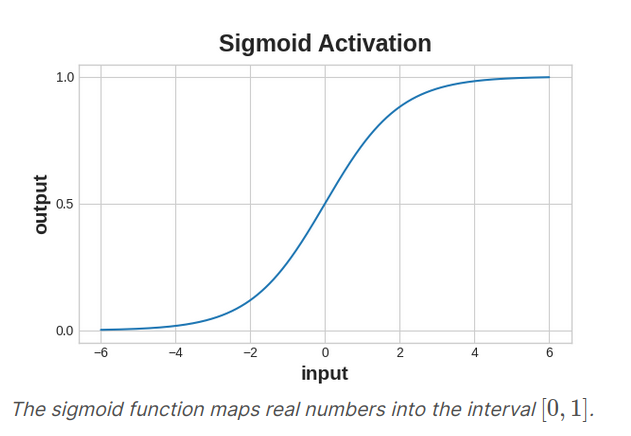
To get the final class prediction, we define a threshold probability. Typically this will be 0.5, so that rounding will give us the correct class : below 0.5 means the class with label 0, 0.5 or above means the class with label 1.
from tensorflow import keras
from tensorflow.keras import layers
model = keras.Sequential([
layers.Dense(4, activation='relu', input_shape=[33]),
layers.Dense(4, activation='relu'),
layers.Dense(1, activation='sigmoid'),
])
In the final layer, it include a sigmoid activation so that the model will produce class probabilities. Add the cross-entropy loss and accuracy metric to the model with its compile method.
model.compile(
optimizer='adam',
loss='binary_crossentropy',
metrics=['binary_accuracy'],
)
The model in this particular problem can take quite a few epoches to complete training, so we'll include an early stopping callbacks for convenience.
early_stopping = keras.callbacks.EarlyStopping(
patience=10,
min_delta=0.001,
restore_best_weights=True,
)
history = model.fit(
X_train, y_train,
validation_data=(X_valid, y_valid),
batch_size=512,
epochs=1000,
callbacks=[early_stopping],
verbose=0, # hide the output because we have so many epochs
)
Source from : https://www.kaggle.com/learn
'Data Science > Neural Network' 카테고리의 다른 글
| [Tensorflow] Dropout and Batch Normalization (1) | 2022.09.22 |
|---|---|
| [Tensorflow] Overfitting and Underfitting (0) | 2022.09.21 |
| [Tensorflow] Stochastic Gradient Descent (0) | 2022.09.21 |
| [Tensorflow] Deep Neural Networks (0) | 2022.09.21 |
| [Tensorflow] A Single Neuron (0) | 2022.09.20 |



