1. QDA(Quardratic Discriminant Analysis)
- QDA assumes that each class has its own covariance matrix, \(X ~ N(\mu_k, \sum _ k)\)
- LDA vs QDA
- Probability : \(P(y_i=k|x)\)
- X : \(N(\mu_k,\sum)\) vs \(N(\mu_k, \sum_k)\)
- Parameters : \(\mu_1, ..., \mu_k$ vs $\mu_1, ..., \mu_k, \sum_1, ..., \sum_k\)
- Num of grids : \(PK + \frac{P(P+1)}{2}$ vs $PK + K\frac{P(P+1)}{2}\)
1.1 [Ex] LDA vs QDA
Classification Error Rate of LDA
# Import library
library(ISLR)
data(Default)
attach(Default)
library(MASS)
# Train-test split
set.seed(1234)
n <- length(default)
train <- sample(1:n, n*0.7)
test <- setdiff(1:n, train)
# Classification error rate of LDA
g1 <- lda(default~., data=Default, subset=train)
pred1 <- predict(g1, Default)
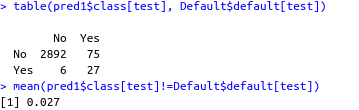
table(pred1$class[test], Default$default[test])
mean(pred1$class[test]!=Default$default[test])
Classification Error Rate of QDA
# Classification error rate of QDA
g2 <- qda(default~., data=Default, subset=train)
pred2 <- predict(g2, Default)
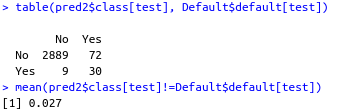
table(pred2$class[test], Default$default[test])
mean(pred2$class[test]!=Default$default[test])
AUC Score between LDA and QDA
# AUC comparison between LDA and QDA
library(ROCR)
label <- factor(default[test], levels=c("Yes","No"),
labels=c("TRUE","FALSE"))
preds1 <- prediction(pred1$posterior[test,2], label)
preds2 <- prediction(pred2$posterior[test,2], label)
performance(preds1, "auc")@y.values
performance(preds2, "auc")@y.values
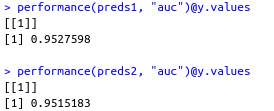
Performance of applying LDA works better than QD.
Simulation study of LDA and QDA iterating 100 times
# Simulation Study
set.seed(123)
N <- 100
CER <- AUC <- matrix(NA, N, 2)
for (i in 1:N) {
train <- sample(1:n, n*0.7)
test <- setdiff(1:n, train)
y.test <- Default$default[test]
g1 <- lda(default~., data=Default, subset=train)
g2 <- qda(default~., data=Default, subset=train)
pred1 <- predict(g1, Default)
pred2 <- predict(g2, Default)
CER[i,1] <- mean(pred1$class[test]!=y.test)
CER[i,2] <- mean(pred2$class[test]!=y.test)
label <- factor(default[test], levels=c("Yes","No"), labels=c("TRUE","FALSE"))
preds1 <- prediction(pred1$posterior[test,2], label)
preds2 <- prediction(pred2$posterior[test,2], label)
AUC[i,1] <- as.numeric(performance(preds1, "auc")@y.values)
AUC[i,2] <- as.numeric(performance(preds2, "auc")@y.values)
}
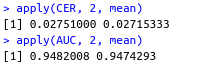
apply(CER, 2, mean)
apply(AUC, 2, mean)
2. Naive Bayes Method
- Assumes that features are independent in each class.
- Useful when p is large.
- Gaussian naive Bayes assumes each \(\sum_k\) is diagonal.
- Despite strong assumptions, NB method often produces good classification results.
2.1 [Ex] Naive Bayes of Iris dataset
Calculate Train Error
# Import library and data
data(iris)
library(e1071)
# Train model
# g1 <- naiveBayes(Species ~ ., data=iris)
g1 <- naiveBayes(iris[,-5], iris[,5])
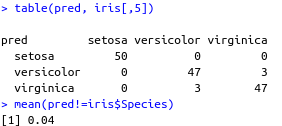
pred <- predict(g1, iris[,-5])
table(pred, iris[,5])
mean(pred!=iris$Species)
Validation Set
# Randomly separate training sets and test sets
set.seed(1234)
tran <- sample(nrow(iris), size=floor(nrow(iris)*2/3))
# Compute misclassification error for test sets
g2 <- naiveBayes(Species ~ ., data=iris, subset=tran)
pred2 <- predict(g2, iris)[-tran]
test <- iris$Species[-tran]
table(pred2, test)
mean(pred2!=test)

2.2 [Ex] Naive Bayes of default dataset
Calculate Missclassification Error Rate of Test-set
# Import dataset
data(Default)
# Train-test split
set.seed(1234)
n <- nrow(Default)
train <- sample(1:n, n*0.7)
test <- setdiff(1:n, train)
# train model and calculate missclassification rate
g3 <- naiveBayes(default ~ ., data=Default, subset=train)
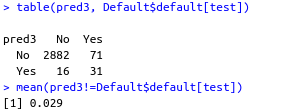
pred3 <- predict(g3, Default)[test]
table(pred3, Default$default[test])
mean(pred3!=Default$default[test])
AUC of Naive Bayes
# AUC of Naive Bayes
library(ROCR)
label <- factor(default[test], levels=c("Yes","No"), labels=c("TRUE","FALSE"))
pred4 <- predict(g3, Default, type="raw")
preds <- prediction(pred4[test, 2], label)
performance(preds, "auc")@y.values
The performance of model : 0.9454898
3. KNN(K-Nearest Neighbors)
- Predict qualitative response using the Bayes classifier.
- KNN classifier estimates the conditional distribution of
- \(Pr(Y=j|X=x_0) = \frac{1}{K}\sum_{i \in N_0} I(y_i=j)\)
- \(x_0\) : a test observation
- \(N_0\) : a set of K points in the training data that are closest to \(x_0\).
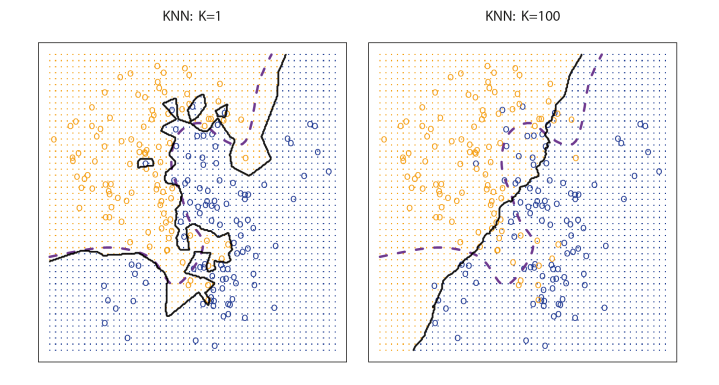
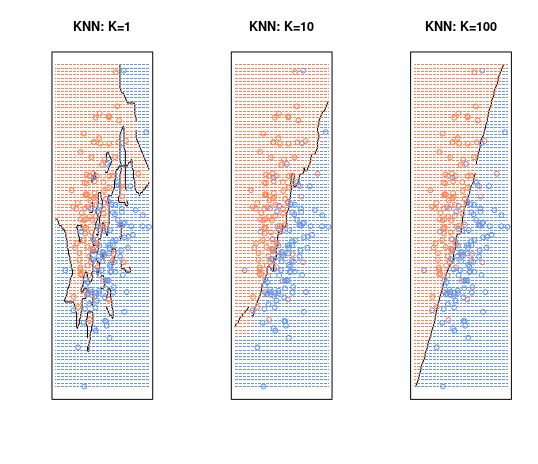
- KNN decision boundary(black) and The Bayesian decision boundary(purple).
- The choice of \(K\) has a drastic effect on the KNN classifier.
- When K=1, the decision boundary is overfitting(low bias + high variance).
- When K=100, the decision boundary is underfitting(high bias + low variance).
- We need to find the best \(K\) which optimizes the test error rate.
3.1 [Ex] Caran Insurance Dataset
Prepare dataset
# Importing library and data
library(ISLR)
data(Caravan)
dim(Caravan)
str(Caravan)
attach(Caravan)
# only 6% of people purchased caravan insurance.
summary(Purchase)
mean(Purchase=="Yes")
Training Logistic Regression
# Logistic regression
g0 <- glm(Purchase~., data=Caravan, family="binomial")
summary(g0)
Training glmnet with CV
library(glmnet)
y <- Purchase
x <- as.matrix(Caravan[,-86])
# glmnet with cross validation
set.seed(123)
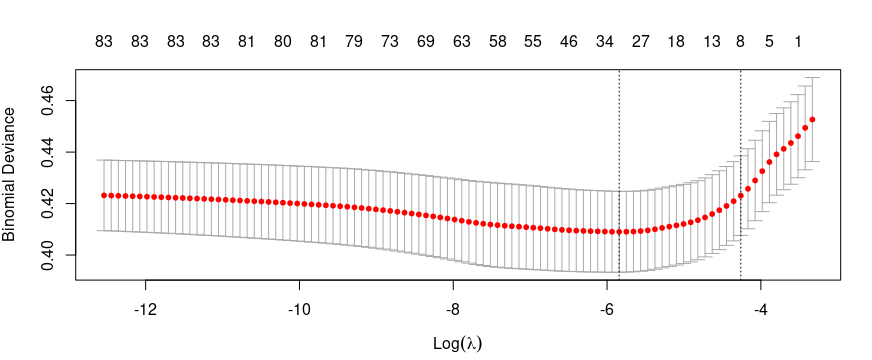
g1.cv <- cv.glmnet(x, y, alpha=1, family="binomial")
plot(g1.cv)
# Extract the value of lambda of model g1.cv
g1.cv$lambda.min
g1.cv$lambda.1se
# Check coefficients
coef1 <- coef(g1.cv, s="lambda.min")
coef2 <- coef(g1.cv, s="lambda.1se")
cbind(coef1, coef2)
# Degree of freedom
sum(coef1!=0)-1
sum(coef2!=0)-1
Degree of freedom
- lambda.min = 31
- lambda.1se = 8
KNN methods
# Standardize data so that mean=0 and variance=1.
X <- scale(Caravan[,-86])
apply(Caravan[,1:5], 2, var)
apply(X[,1:5], 2, var)
# Separate training sets and test sets
test <- 1:1000
train.X <- X[-test, ]
test.X <- X[test, ]
train.Y <- Purchase[-test]
test.Y <- Purchase[test]
## Classification error rate of KNN
set.seed(1)
knn.pred <- knn(train.X, test.X, train.Y, k=1)
mean(test.Y!=knn.pred)
mean(test.Y!="No")
table(knn.pred, test.Y)
knn.pred=knn(train.X, test.X, train.Y, k=3)
table(knn.pred, test.Y)
mean(test.Y!=knn.pred)
knn.pred=knn(train.X, test.X, train.Y, k=5)
table(knn.pred, test.Y)
mean(test.Y!=knn.pred)
knn.pred=knn(train.X, test.X, train.Y, k=10)
table(knn.pred, test.Y)
mean(test.Y!=knn.pred)

3.2 [Ex] KNN with Hyperparameter Tuning of K based on Validation set
# Import dataset
library(ISLR)
data(Caravan)
attach(Caravan)
library(class)
# Train-Test Splitting : Train-Validation-Test set
set.seed(1234)
n <- nrow(Caravan)
s <- sample(rep(1:3, length=n))
tran <- s==1
valid <- s==2
test <- s==3
# Hyperparameter of K
K = 100
# Train-Test Splitting : Train-Validation-Test set
X <- scale(Caravan[,-86])
y <- Caravan[,86]
train.X <- X[tran,]
valid.X <- X[valid,]
test.X <- X[test,]
train.y <- y[tran]
valid.y <- y[valid]
test.y <- y[test]
# Calculate Missclassification Error rate of validation set
miss <- rep(0, K)
for (i in 1:K) {
knn.pred <- knn(train.X, valid.X, train.y, k=i)
miss[i] <- mean(valid.y != knn.pred)
}
miss
wm <- which.min(miss)
# Calculate Missclassifiaction Error rate of test set
miss_test <- knn(train.X, test.X, train.y, k=wm)
mean(test.y != miss_test)
- The optimized value of K is 8, and its missclassification error rate is 0.06134021.
3.3 [Ex] KNN Simulation Study
# Import dataset
library(ISLR)
data(Caravan)
attach(Caravan)
library(class)
# Simulation
library(mnormt)
set.seed(1010)
sigma <- matrix(c(1, 0.5, 0.5, 1), 2, 2)
x.tran1 <- rmnorm(100, c(0, 0.8), sigma)
x.tran2 <- rmnorm(100, c(0.8, 0), sigma)
x.test1 <- rmnorm(3430, c(0, 0.8), sigma)
x.test2 <- rmnorm(3430, c(0.8 ,0), sigma)
x.tran <- rbind(x.tran1, x.tran2)
x.test <- rbind(x.test1, x.test2)
y.tran <- factor(rep(0:1, each=100))
mn <- min(x.tran)
mx <- max(x.tran)
px1 <- seq(mn, mx, length.out=70)
px2 <- seq(mn, mx, length.out=98)
gd <- expand.grid(x=px1, y=px2)
# Training model
g1 <- knn(x.tran, gd, y.tran, k = 1, prob=TRUE)
g2 <- knn(x.tran, gd, y.tran, k = 10, prob=TRUE)
g3 <- knn(x.tran, gd, y.tran, k = 100, prob=TRUE)
# Visualization of K=1
par(mfrow=c(1,3))
prob1 <- attr(g1, "prob")
prob1 <- ifelse(g1=="1", prob1, 1-prob1)
pp1 <- matrix(prob1, length(px1), length(px2))
contour(px1, px2, pp1, levels=0.5, labels="", xlab="", ylab="",
main="KNN: K=1", axes=FALSE)
points(x.tran, col=ifelse(y.tran==1, "cornflowerblue", "coral"))
co1 <- ifelse(pp1>0.5, "cornflowerblue", "coral")
points(gd, pch=".", cex=1.2, col=co1)
box()
# Visualization of K=10
prob2 <- attr(g2, "prob")
prob2 <- ifelse(g2=="1", prob2, 1-prob2)
pp2 <- matrix(prob2, length(px1), length(px2))
contour(px1, px2, pp2, levels=0.5, labels="", xlab="", ylab="",
main="KNN: K=10", axes=FALSE)
points(x.tran, col=ifelse(y.tran==1, "cornflowerblue", "coral"))
co2 <- ifelse(pp2>0.5, "cornflowerblue", "coral")
points(gd, pch=".", cex=1.2, col=co2)
box()
# Visualization of K = 100
prob3 <- attr(g3, "prob")
prob3 <- ifelse(g3=="1", prob3, 1-prob3)
pp3 <- matrix(prob3, length(px1), length(px2))
contour(px1, px2, pp3, levels=0.5, labels="", xlab="", ylab="",
main="KNN: K=100", axes=FALSE)
points(x.tran, col=ifelse(y.tran==1, "cornflowerblue", "coral"))
co3 <- ifelse(pp3>0.5, "cornflowerblue", "coral")
points(gd, pch=".", cex=1.2, col=co3)
box()
When the graph according to the value of K is checked, it can be seen that the decision boundary is overfitting when K = 1. If K = 100, the decision boundary is briefly drawn. It can be seen that K = 10 forms an appropriate decision boundary.
'Data Science > R' 카테고리의 다른 글
| [R] Non-Linear Models : Step Functions (0) | 2022.11.14 |
|---|---|
| [R] Non-Linear Models : Polynomials (0) | 2022.11.14 |
| [R] Assessment of the Performance of Classifier (0) | 2022.11.05 |
| [R] Classification Problem : LDA(Linear Discriminant Analysis) (0) | 2022.10.31 |
| [R] Classification Problem : Logistic Regression (0) | 2022.10.18 |



