1. What is Feature Engineering?
Feature Engineering is the process of using domain knowledge to extract features from raw data. The motivation is to use these extra features to improve the quality of resuls from a machine learning process, compared with supplying only the raw data to the machine learning process.
2. Mutual Information
Mutual Information is a lot like correlation in that it measures a relationship between two quantities. The advantages of mutual information is that it can detect any kind of relationship, whlie correlation only detects linear relationships.
Mutual information is a great general purpose metric and especially useful at the start of feature development when you might now know what model you'd like to use yet.
Mutual information describes relationships in terms of uncertainty. The mutual information between two quantities is a measure of the extent to which knowledge of one quality reduces uncertainty about the other.
The least possible mutual information between quantities is 0.0. When MI is zero, the quantities are independent : neither can tell we anything about the other. Conversly, in theory, there's no upper bound to what MI can be. In practice, values above 2.0 or so are uncommon.
What we need to focus is following :
- The scikit-learn algorithm for MI treats discrete feature differently from continuous features. Consequently, we need to tell it which are which. As a rule of thumb, anything that must have a float dtypes is not discrete. Categorical can be treated by giving them a label encoding.
- Scikit-learn has two mutual information metrics in its feature_selection module : One for real-valued traget and the other for categorical targets.
from sklearn.feature_selection import mutual_info_regression
def make_mi_scores(X, y, discrete_features):
mi_scores = mutual_info_regression(X, y, discrete_features=discrete_features)
mi_scores = pd.Series(mi_scores, name="MI Scores", index=X.columns)
mi_scores = mi_scores.sort_values(ascending=False)
return mi_scores
def plot_mi_scores(scores):
scores = scores.sort_values(ascending=True)
width = np.arange(len(scores))
ticks = list(scores.index)
plt.barh(width, scores)
plt.yticks(width, ticks)
plt.title("Mutual Information Scores")
3. Creating Features
Tips on Discovering New Features
First, understand the features. Reger to our dataset's data documentation if available.
Second, research the problem domain to acquire domain knowledge. If our problem is predicting house price, do some research on real-estate for instance. Wikipedia can be a good starting point, but books and journal articles willl often have the best information.
Third, study previous work. Solution write-ups from past works are a great resource.
At last, use data visualization. Visualization can reveal pathologies in the distribution of a feature or complicated relationships that could simplified.
Mathematcial Transforms
Relationships among numerical features are often expressed through mathematical formulas, which we'll frequently come across as part of our domain research. In Pandas, we can apply arithmetic operations to columns just as if they were ordinary numbers. Data visualization can suggest transformations, often a "reshaping" of a feature through powers or logarithms.
Counts
Features describing the presence or absence of something often come in sets, the set of risk factor for disease, say. You can aggregate such features by creating a count. These features will be binary or boolean. In Python, boolean can be added up just as if they were integers.
Building-Up and Breaking-Down Features
Features like phone number will often have some kind of structure that we can make use of. US phone number, for instance, can tell us the location of the caller.
Group Transform
Group transform aggregate information across multiple rows grouped by some category. With a group transform we can create features like : "the average income of a person's state of residence", or "the proportion of movies released on a weekday, by genre".
Using an aggergation function, a group transform combines two features : a categorical features that provides the grouping and another feature whose value we wish to aggregate. To compute this in Pandas, we can use the group by and transform method.
# Mathematical Tranform
autos["displacement"] = (
np.pi * ((0.5 * autos.bore) ** 2) * autos.stroke * autos.num_of_cylinders
)
# If the feature has 0.0 values, use np.log1p (log(1+x)) instead of np.log
accidents["LogWindSpeed"] = accidents.WindSpeed.apply(np.log1p)
# Plot a comparison
fig, axs = plt.subplots(1, 2, figsize=(8, 4))
sns.kdeplot(accidents.WindSpeed, shade=True, ax=axs[0])
sns.kdeplot(accidents.LogWindSpeed, shade=True, ax=axs[1]);
# Counts
roadway_features = ["Amenity", "Bump", "Crossing", "GiveWay",
"Junction", "NoExit", "Railway", "Roundabout",
"Station", "Stop", "TrafficCalming", "TrafficSignal"]
accidents["RoadwayFeatures"] = accidents[roadway_features].sum(axis=1)
# Group Transform
customer["AverageIncome"] = customer.groupby("State")["Income"].transform("mean")
# Frequency of categorical value
customer["StateFreq"] = customer.groupby("State")["State"].transform("count") / customer.State.count()
4. Clustering
4.1 What is Clustering?
Clustering simply means the assigning of data points to group based upon how similar the points are to each other. A clustering algorithm makes "birds of flock together", so to speak.
When used for feature engineering, we could attempt to discover groups of customers representing a market segment, for instance, or geographic areas that share similar weather patterns. Adding a feature of clustering label can help machine learning models untangle complicated relationship of space or proximity.
Applied to a single real-valued feature, clustering acts like a traditional "binnint" or "discretization" transform. On multiple features, it's like "multi dimensional binning".
It's important to remember that this clustering feature is a categorical. The motivating idea of adding cluster labels is that the clusters will break up complicated relationships across features into simpler chunks. Our model can then just learn the simpler chunks one-by-one instead having to learn the complicated whole at once.
4.2 K-means Clustering
K-means clustering measures similarity using ordinary straight-line distance (Euclidean distance). It creates clusters by placing a number of points, called centroids, inside the feature-space. Each point in the dataset is assigned to the cluster of whichever centroid it's closest to. The "K" in "K-means" is how many centroids it create.
We could imagine each centroid capturing points through a sequence of radiating circles. When sets of circle from competing centroids overlap , they form a line. The result is what's called a voronoi tessalation. The tessalation shows us to what clusters future data will be assigned.
When we implement clustering algorith, there are two step processes.
- Assign points to the nearest cluster centroid
- Move each centroid to minimize the distance to its points
It iterates over these two steps until the centroid aren't moving anymore, or until some maximum number of iterations has passed. (There is parameter named max_iter in centroid function.)
It often happens that the initial random posistion of the centroids ends in a poor clustering. For this reason the algorithm repeats a number of times (There is a parameter named n_init in centroid function) and returns the clustering that has the least total distance between each point and its centroid, the optimal clustering.
We may need to increase the max_iter for a large number of clusters or n_init for a complex dataset. Ordinarily though the only parameter we'll need to choose ourself is n_cluster(K). The best partitioning for a set of features depends on the model we're using and what we're trying to predict, so it's best to tune it like any hyperparameter.
kmeans = KMeans(n_clusters = 6)
X['Cluster'] = kmeans.fit_predict(X)
X['Clutser'] = X['Cluster'].astype('category')
5. Principal Component Analysis : PCA
PCA is a great tool to help us discover important relationships in the data and can also be used to create more informative features. It is typically applied to standardized data. With standardized data "variation" means "correlation". With unstandardized data "variation" means "covariance".
There are two ways we could use PCA for feature engineering.
The first way is to use it as a descriptive technique. Since the componenets tell us about the variation, we could compute the MI scores for the components and see what kind of variation is most predictive of our target. That could give us ideas for kinds of feature to create.
The second way is to use the components themselves as a feature. Because the components expose the variation structure of the data directly, they can often be more informative than the original features.
- Dimensionality reduction : When our features are highly redundant, PCA will partition out the redundancy into one or more near-zero variance components, which we can then drop since they will contain little or no information.
- Anomaly Detection : Unusual variation, not apparent from the original features, will often show up in the low-variance components. These components could be highly informative in an anomaly or outlier detection task.
- Noise reduction : A collection of sensor reading will often share some common background noise. PCA can sometimes collect the signal into a small number of features while leaving the noise alone, thus boosting the signal-to-noise ratio.
- Decorrelation : Some ML algorithms struggle with highly correlated features. PCA transforms correlated features into uncorrelated components, which could be easier for our algorithm to work with.
X = df.copy()
# Divide data into X and y
features = ['highway_mpg', 'engine_size', 'horsepower', 'curb_weight']
y = X.pop('price')
X = X.loc[:, features]
# Standardize
X_scaled = (X-X.mean(axis = 0)) / X.std(axis = 0)
# Create principal components
from sklearn.decomposition import PCA
pca = PCA()
X_pca = pca.fit_transform(X_scaled)
# Convert to dataframe
component_names = [f"PC{i+1}" for i in range(X_pcc.shape[1])]
X_pca = pd.DataFrame(X_pca, columns = component_names)
After fitting, the PCA instance contains the loadings in its components ._attribute.
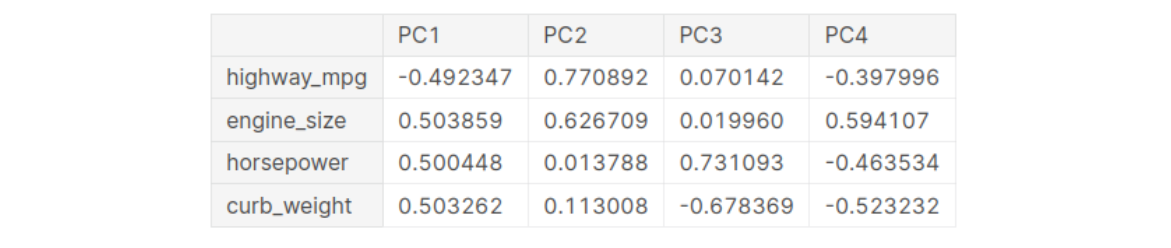
Recall that the signs and magnitudes of a component's loadings tell us what kind of variation it's captured. The first component show a contrast between large, powerful vehicles with poor gas milage, and smaller, more economical vehicles with good gas milage. We might call this the "Luxury/Economy" axis. The next figure shows that our four chosen features mostly vary along the Luxury/Economy axis.
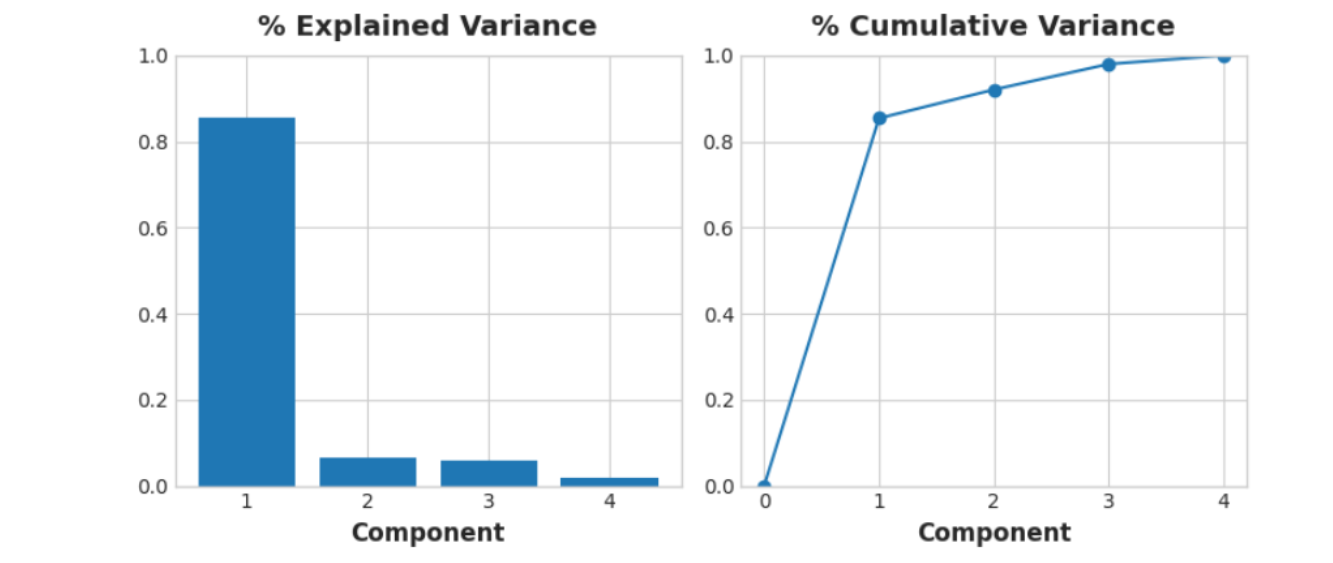
Let's also look at the MI scores of the components. Not surprisingly, PC1 is highly informative, though the remaining components, despite their smaller variance, still have significant relationship with price. Examining those components could be worthwile to find relationships not captured by the main Luxury/Economy axis.
| Components | MI Score |
| PC1 | 1.013800 |
| PC2 | 0.379440 |
| PC3 | 0.306502 |
| PC4 | 0.204447 |
Source from :
'Data Science > Scikit-Learn' 카테고리의 다른 글
| [Sklearn] Transforming Columns by its Type (0) | 2022.09.20 |
|---|---|
| [Sklearn] Scalers (0) | 2022.09.20 |
| [Sklearn] Dealing Categorical Variables : Encoders (0) | 2022.09.20 |
| [Sklearn] Dealing Missing Values : Imputers (0) | 2022.09.20 |
| [Sklearn] Cross Validation (0) | 2022.09.20 |